With each update of Dynamics 365 Business Central, Microsoft enhances what is often referred to as the base application and enhances the development environment. Dynamics 365 Business Central 2023 Wave 1 has several exciting Development features for runtime 11.0. One of the exciting features is to Attach AL debugger to active session or next session.
In any development environment, debugging is one part of the development lifecycle. Developing in AL for Microsoft Dynamics 365 Business Central is no different.
What is debugging?
Debugging is finding and resolving errors or defects within a computer program. Debugging aims to identify and fix bugs, which are issues or problems that prevent the program from functioning as intended. Debugging is an essential part of the software development process, as it ensures that the program is working correctly and meets the requirements of the end users.
Debugging can involve various techniques and tools, including step-by-step execution, logging, tracing, and testing. Developers use debugging tools such as debuggers, profilers, and log analyzers to help identify and resolve issues within the code. They may also use code review and collaboration tools to help identify and resolve problems.
Debugging helps the program runs efficiently, accurately, and as intended. By carefully identifying and fixing bugs, developers can improve the quality and reliability of their software.
Debugging Microsoft Dynamics 365 Business Central
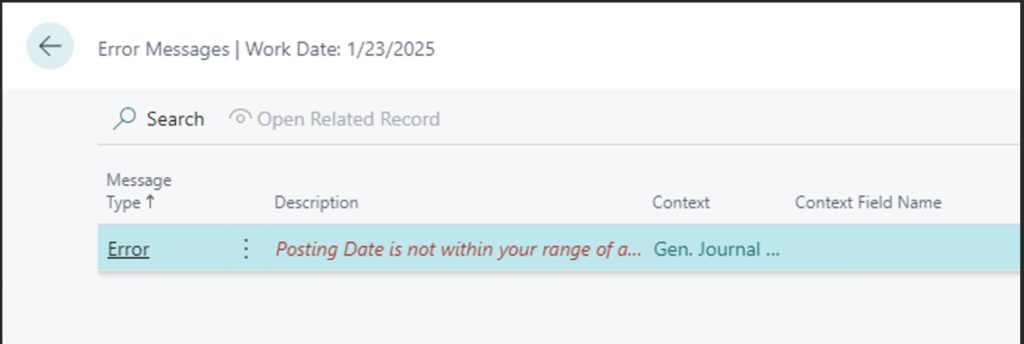
AL Developers can debug code execution in Business Central by attaching a session to a specified server and awaiting a process to trigger your set breakpoint or the trigger of an error. Then debugging starts when the code on which the breakpoint is executed or a statement generates an error.
To activate the attach functionality, you need to create a new configuration in the launch.json file. This configuration comes in two flavors: Attach to the next client on the cloud sandbox and Attach to the next client on your server. If you want to attach to a cloud session, use the first option; if you’re going to attach to a local server, use the second option.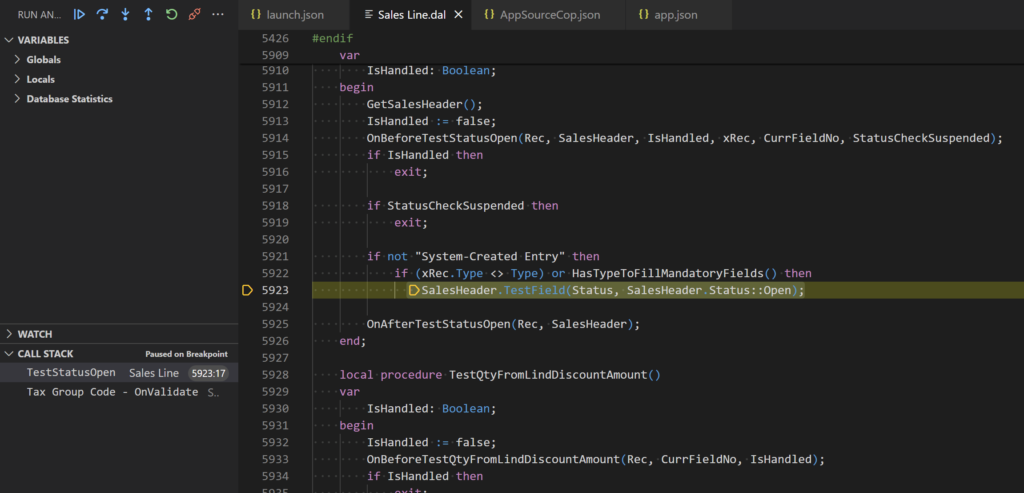
In the attach configuration, the breakOnNext setting specifies the next client to break on when the debugging session starts and allows only one option. The available options are: WebServiceClient, WebClient, and Background. The example below illustrates a configuration for a local server.
New Debugging Microsoft Dynamics 365 Business Central 2023 Wave 1
Starting with Microsoft Dynamics 365 Business Central 2023 Wave 1, two new settings, userId, and sessionID, were added to the launch.json configuration allowing you to specify a session ID to attach to an existing session or a user ID to attach to the next session for that user. These new settings allow the standard AL debugger to connect to a currently running session or the next session for the specific user.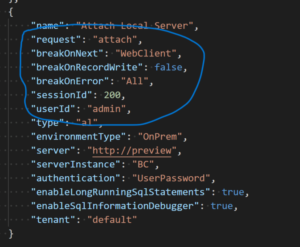
Read more about the feature Attach AL debugger to active session or next session here.
Read more about debugging in AL for Microsoft Dynamics 365 Business Central here.
Note: The code and information discussed in this article is for informational and demonstration purposes only. This content was created referencing Microsoft Dynamics 365 Business Central 2023 Wave 1 online.




 available.
available.